 | ||
 |
RFワールド読者の掲示板Ⅱ
無線と高周波に関することを中心に、それ以外の話題も含めて、何でも書き込みOKの掲示板です。初めての方もネチケットを守って、お気軽にご参加下さい(^^)/
| ▼ | 長岡係数 森のカエル 21/1/26(火) 20:26 |
| Re:長岡係数 Joe 21/1/28(木) 12:20 |
|
| Re:長岡係数 森のカエル 21/1/28(木) 13:18 |
| Re:長岡係数 Joe 21/1/31(日) 16:35 |
| Re:長岡係数 森のカエル 21/2/3(水) 19:13 |
| [管理人削除] |
| Re:長岡係数 森のカエル 21/2/3(水) 19:08 |
| Re:長岡係数 森のカエル 21/2/4(木) 0:08 |
|
| Re:長岡係数 森のカエル 21/2/4(木) 1:15 |
|
| Re:長岡係数 M2019J1 21/8/26(木) 21:25 |
| Re:長岡係数 森のカエル 21/8/29(日) 10:01 |
| Re:長岡係数 森のカエル 21/9/28(火) 18:33 |
|
森のカエル - 21/1/26(火) 20:26 - |
コイルのインダクタンス算出の「長岡係数」について、
割と簡単な近似式を見つけました。とても簡単なので既知なのでは?と
思うのですが、ご存知でしょうか??
直径÷長さ を x とするとき、
長岡係数 ≒ ( 2 / (2 + x ) )^0.9
あるいは、長岡係数 ≒ ( 長さ ÷(半径+長さ))^0.9
https://ja.wikipedia.org/wiki/長岡係数
の表の値に対して、Est の列が近似値。
x 長岡係数 Est error
0.0 1.000 1.00000 0.0000e+00
0.1 0.959 0.95704 2.0490e-03
0.2 0.920 0.91780 2.4004e-03
0.3 0.884 0.88180 2.4906e-03
0.4 0.850 0.84867 1.5717e-03
0.5 0.818 0.81805 -6.3744e-05
0.6 0.789 0.78968 -8.6075e-04
0.7 0.761 0.76331 -3.0232e-03
0.8 0.735 0.73873 -5.0470e-03
0.9 0.711 0.71576 -6.6534e-03
1.0 0.688 0.69425 -9.0070e-03
1.2 0.648 0.65508 -1.0803e-02
1.5 0.595 0.60432 -1.5420e-02
2.0 0.526 0.53589 -1.8449e-02
3.0 0.429 0.43838 -2.1404e-02
4.0 0.356 0.37204 -4.3116e-02
6.0 0.285 0.28717 -7.5724e-03
8.0 0.237 0.23492 8.8378e-03
10.0 0.203 0.19937 1.8198e-02
>
割と簡単な近似式を見つけました。とても簡単なので既知なのでは?と
思うのですが、ご存知でしょうか??
直径÷長さ を x とするとき、
長岡係数 ≒ ( 2 / (2 + x ) )^0.9
あるいは、長岡係数 ≒ ( 長さ ÷(半径+長さ))^0.9
https://ja.wikipedia.org/wiki/長岡係数
の表の値に対して、Est の列が近似値。
x 長岡係数 Est error
0.0 1.000 1.00000 0.0000e+00
0.1 0.959 0.95704 2.0490e-03
0.2 0.920 0.91780 2.4004e-03
0.3 0.884 0.88180 2.4906e-03
0.4 0.850 0.84867 1.5717e-03
0.5 0.818 0.81805 -6.3744e-05
0.6 0.789 0.78968 -8.6075e-04
0.7 0.761 0.76331 -3.0232e-03
0.8 0.735 0.73873 -5.0470e-03
0.9 0.711 0.71576 -6.6534e-03
1.0 0.688 0.69425 -9.0070e-03
1.2 0.648 0.65508 -1.0803e-02
1.5 0.595 0.60432 -1.5420e-02
2.0 0.526 0.53589 -1.8449e-02
3.0 0.429 0.43838 -2.1404e-02
4.0 0.356 0.37204 -4.3116e-02
6.0 0.285 0.28717 -7.5724e-03
8.0 0.237 0.23492 8.8378e-03
10.0 0.203 0.19937 1.8198e-02
>
1,600 hits
|
Joe - 21/1/28(木) 12:20 - |
▼森のカエルさん:
> コイルのインダクタンス算出の「長岡係数」について、
> 割と簡単な近似式を見つけました。とても簡単なので既知なのでは?と
> 思うのですが、ご存知でしょうか??
Wikipediaに書いてある近似式よりはるかにシンプルですね。
どれぐらい誤差があるかをグラフ化してみてびっくり!
形状比4のあたりは-4%ほどありますが、これぐらいのずれならコイルを自分で巻くのに十分使えると思います。
特に形状比1以下の長い円筒状コイルなら誤差1%以下ですね。
この近似式はどなたが考案されたものでしょう?すばらしいです。
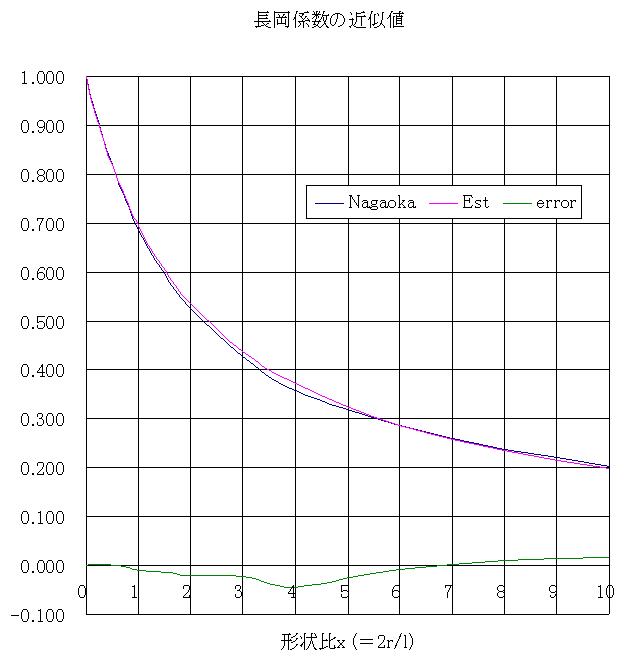
【915_NagaokaCoeff-estimated-20210128.gif : 12.9KB】
> コイルのインダクタンス算出の「長岡係数」について、
> 割と簡単な近似式を見つけました。とても簡単なので既知なのでは?と
> 思うのですが、ご存知でしょうか??
Wikipediaに書いてある近似式よりはるかにシンプルですね。
どれぐらい誤差があるかをグラフ化してみてびっくり!
形状比4のあたりは-4%ほどありますが、これぐらいのずれならコイルを自分で巻くのに十分使えると思います。
特に形状比1以下の長い円筒状コイルなら誤差1%以下ですね。
この近似式はどなたが考案されたものでしょう?すばらしいです。

【915_NagaokaCoeff-estimated-20210128.gif : 12.9KB】
1,121 hits
|
森のカエル - 21/1/28(木) 13:18 - |
▼Joeさん:
>▼森のカエルさん:
>> コイルのインダクタンス算出の「長岡係数」について、
>> 割と簡単な近似式を見つけました。とても簡単なので既知なのでは?と
>> 思うのですが、ご存知でしょうか??
> どれぐらい誤差があるかをグラフ化してみてびっくり!
> 形状比4のあたりは-4%ほどありますが、これぐらいのずれならコイルを自分で巻くのに十分使えると思います。
> 特に形状比1以下の長い円筒状コイルなら誤差1%以下ですね。
> この近似式はどなたが考案されたものでしょう?
えへん、
私の考案? です
2マイクロヘンリ程のコイルを手巻きしようとしたついでに
色々と数字をいじっていて発見しました.
最適化していないのですが、結構な精度だし、
暗記しやすい長所が優ると思います。
でも、歴史も知名度もある長岡係数、きっと誰か先人がいそう。
>▼森のカエルさん:
>> コイルのインダクタンス算出の「長岡係数」について、
>> 割と簡単な近似式を見つけました。とても簡単なので既知なのでは?と
>> 思うのですが、ご存知でしょうか??
> どれぐらい誤差があるかをグラフ化してみてびっくり!
> 形状比4のあたりは-4%ほどありますが、これぐらいのずれならコイルを自分で巻くのに十分使えると思います。
> 特に形状比1以下の長い円筒状コイルなら誤差1%以下ですね。
> この近似式はどなたが考案されたものでしょう?
えへん、
私の考案? です
2マイクロヘンリ程のコイルを手巻きしようとしたついでに
色々と数字をいじっていて発見しました.
最適化していないのですが、結構な精度だし、
暗記しやすい長所が優ると思います。
でも、歴史も知名度もある長岡係数、きっと誰か先人がいそう。
1,123 hits
|
Joe - 21/1/31(日) 16:35 - |
▼森のカエルさん:
>えへん、
>私の考案? です
おお,森のカエルさんご自身の考案でしたか!素晴らしいです.
>2マイクロヘンリ程のコイルを手巻きしようとしたついでに
>色々と数字をいじっていて発見しました.
2μHだと短波帯あたりの空芯コイルですね.
>でも、歴史も知名度もある長岡係数、きっと誰か先人がいそう。
どうでしょうね.1970年代以前だとノモグラフが幅を
効かせていたので,意外と近似式を模索する人は少なかった
かもしれないと思います.
電子回路ハンドブックとか,無線工学ハンドブック
みたいな本に掲載する価値があると思いますよ.
>えへん、
>私の考案? です
おお,森のカエルさんご自身の考案でしたか!素晴らしいです.
>2マイクロヘンリ程のコイルを手巻きしようとしたついでに
>色々と数字をいじっていて発見しました.
2μHだと短波帯あたりの空芯コイルですね.
>でも、歴史も知名度もある長岡係数、きっと誰か先人がいそう。
どうでしょうね.1970年代以前だとノモグラフが幅を
効かせていたので,意外と近似式を模索する人は少なかった
かもしれないと思います.
電子回路ハンドブックとか,無線工学ハンドブック
みたいな本に掲載する価値があると思いますよ.
1,189 hits
|
- - |
この書き込みは管理人によって削除されました。(21/2/3(水) 18:58)
1,083 hits
|
森のカエル - 21/2/3(水) 19:08 - |
▼M2019J1さん:
森のカエルです。
長岡係数の近似計算で、コイル直径 >> 長さのところは考慮外の
計算なので、下記の議論はハズレなのですが・・・
実のところ良い問いかけでして、私も長年疑問に思っています。
「長岡係数をつかうインダクタンスの計算はコイル直径>>長さの場合
どの程度実用的なのだろう??」
と。
極端な例で、ワンターンコイルを計算すると(長さをbとして)
銅線の太さ2mm, 直径 30cmの場合、2r/b = 150なので、
長岡係数は 0.02470 (*1)
つまり L = 0.0247 μ π r^2 /b (*2)
円環コイルとしてその外部インダクタンスを計算すると
L ≒μ r (log(8r/(b/2))-2)
この2つを比べる(μr で割る)と、
0.0247 π r /b = (log(16r/b)-2 )
(r, b) = (150, 2) を入れると、左辺は5.82, 右辺は 5.09。
合わない。(^^; なので、
形状比がこのように大きなときは長岡係数を使った計算は
不適切なのではないかと思うのですが、じゃぁどのあたりから?
なのかが、分かりません。
M2019J1さんも、そんな思いをお持ちなのでは??
この辺がはっきりすれば、
形状比が大きい場合にも使いやすい近似式を探してみよう・・
って気が起きる(かもしれない)のですが。
>無線通信で「マグネチック・ループ」アンテナに人気があります。
>このアンテナは、コイル直径が大きく、長さが最短なので、長岡係数によるインダクタンスの補正値計算に大きく効いてくるのかな、と思ったとこです。
>
>電子回路でも、長さの短いコイルはよく使うので、長岡係数の計算補正効果が実感できるのかな、と思いました。
(*1) https://crystal-set.com/calc/nagaoka.php
(*2) https://jeea.or.jp/course/contents/01157/
を利用しました。
森のカエルです。
長岡係数の近似計算で、コイル直径 >> 長さのところは考慮外の
計算なので、下記の議論はハズレなのですが・・・
実のところ良い問いかけでして、私も長年疑問に思っています。
「長岡係数をつかうインダクタンスの計算はコイル直径>>長さの場合
どの程度実用的なのだろう??」
と。
極端な例で、ワンターンコイルを計算すると(長さをbとして)
銅線の太さ2mm, 直径 30cmの場合、2r/b = 150なので、
長岡係数は 0.02470 (*1)
つまり L = 0.0247 μ π r^2 /b (*2)
円環コイルとしてその外部インダクタンスを計算すると
L ≒μ r (log(8r/(b/2))-2)
この2つを比べる(μr で割る)と、
0.0247 π r /b = (log(16r/b)-2 )
(r, b) = (150, 2) を入れると、左辺は5.82, 右辺は 5.09。
合わない。(^^; なので、
形状比がこのように大きなときは長岡係数を使った計算は
不適切なのではないかと思うのですが、じゃぁどのあたりから?
なのかが、分かりません。
M2019J1さんも、そんな思いをお持ちなのでは??
この辺がはっきりすれば、
形状比が大きい場合にも使いやすい近似式を探してみよう・・
って気が起きる(かもしれない)のですが。
>無線通信で「マグネチック・ループ」アンテナに人気があります。
>このアンテナは、コイル直径が大きく、長さが最短なので、長岡係数によるインダクタンスの補正値計算に大きく効いてくるのかな、と思ったとこです。
>
>電子回路でも、長さの短いコイルはよく使うので、長岡係数の計算補正効果が実感できるのかな、と思いました。
(*1) https://crystal-set.com/calc/nagaoka.php
(*2) https://jeea.or.jp/course/contents/01157/
を利用しました。
1,287 hits
|
森のカエル - 21/2/3(水) 19:13 - |
えへん、えへん。
さしあたり、RFワールドさんに載っけてもらおうかなぁ?
などと・・
でも読者はVUHF以上で、あまり興味ないかな?
CQハムラジオかしら・・
▼Joeさん:
>>でも、歴史も知名度もある長岡係数、きっと誰か先人がいそう。
> どうでしょうね.1970年代以前だとノモグラフが幅を
>効かせていたので,意外と近似式を模索する人は少なかった
>かもしれないと思います.
>
> 電子回路ハンドブックとか,無線工学ハンドブック
>みたいな本に掲載する価値があると思いますよ.
さしあたり、RFワールドさんに載っけてもらおうかなぁ?
などと・・
でも読者はVUHF以上で、あまり興味ないかな?
CQハムラジオかしら・・
▼Joeさん:
>>でも、歴史も知名度もある長岡係数、きっと誰か先人がいそう。
> どうでしょうね.1970年代以前だとノモグラフが幅を
>効かせていたので,意外と近似式を模索する人は少なかった
>かもしれないと思います.
>
> 電子回路ハンドブックとか,無線工学ハンドブック
>みたいな本に掲載する価値があると思いますよ.
1,359 hits
|
森のカエル - 21/2/4(木) 0:08 - |
森のカエルです。
勢いでやってみました。
形状比がx(=2r/b) のときの円環コイルのインダクタンスは
内部インダクタンス Li = μ r / 4
外部インダクタンス Lo = μ r {log(16 r /b)- 2 } =μ r {log(8x)- 2 }
その合計 La = μ r {log(16 r /b) - 1.75 } =μ r {log(8x)-1.75 }
これと長岡係数を使った式
L = K μ r π r N^2 / b = K μ r π x/2
とを見比べて、Lo, La から逆算した長岡係数部分を Ko, Ka とすると
Ko = { log(8x)-2}/(πx/2)
Ka = { log(8x)-1.75} / (πx/2)
Kn として https://crystal-set.com/calc/nagaoka.php に計算してもらった長岡係数、
さらに est = (2/ (2+x))^0.9
これらを並べて表にしたものが下です。
x Kn ko ka est
1 10 0.20332352 0.151644525 0.167560020 0.199371866
2 20 0.12361481 0.097885823 0.105843570 0.115543783
3 50 0.06108325 0.050820905 0.054004004 0.053275065
4 100 0.03465223 0.029823165 0.031414714 0.029052723
5 150 0.02470410 0.021602957 0.022663990 0.020289333
6 200 0.01967690 0.017117938 0.017913713 0.015707634
7 250 0.01678334 0.014262581 0.014899201 0.012872607
8 300 0.01499930 0.012272383 0.012802899 0.010937568
9 350 0.01386311 0.010799572 0.011254300 0.009528808
10 400 0.01313717 0.009662147 0.010060034 0.008455193
11 500 0.01243118 0.008013833 0.008332143 0.006922989
12 800 0.01294981 0.005382663 0.005581606 0.004541194
13 1000 0.01418090 0.004448188 0.004607343 0.003716602
円環コイルとして計算した値が正解だとすると、
形状比 x がとても大きいところでは
Knよりも むしろ est のほうが正解に近い傾向があります。
誤差は2割位と大きいのですが。
グラフの黒い線がKnです。
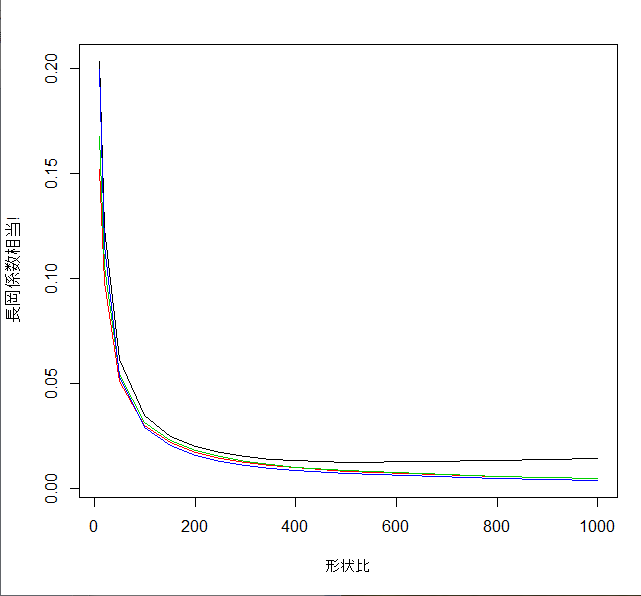
【921_nagaoka_est_bigX.png : 8.4KB】
勢いでやってみました。
形状比がx(=2r/b) のときの円環コイルのインダクタンスは
内部インダクタンス Li = μ r / 4
外部インダクタンス Lo = μ r {log(16 r /b)- 2 } =μ r {log(8x)- 2 }
その合計 La = μ r {log(16 r /b) - 1.75 } =μ r {log(8x)-1.75 }
これと長岡係数を使った式
L = K μ r π r N^2 / b = K μ r π x/2
とを見比べて、Lo, La から逆算した長岡係数部分を Ko, Ka とすると
Ko = { log(8x)-2}/(πx/2)
Ka = { log(8x)-1.75} / (πx/2)
Kn として https://crystal-set.com/calc/nagaoka.php に計算してもらった長岡係数、
さらに est = (2/ (2+x))^0.9
これらを並べて表にしたものが下です。
x Kn ko ka est
1 10 0.20332352 0.151644525 0.167560020 0.199371866
2 20 0.12361481 0.097885823 0.105843570 0.115543783
3 50 0.06108325 0.050820905 0.054004004 0.053275065
4 100 0.03465223 0.029823165 0.031414714 0.029052723
5 150 0.02470410 0.021602957 0.022663990 0.020289333
6 200 0.01967690 0.017117938 0.017913713 0.015707634
7 250 0.01678334 0.014262581 0.014899201 0.012872607
8 300 0.01499930 0.012272383 0.012802899 0.010937568
9 350 0.01386311 0.010799572 0.011254300 0.009528808
10 400 0.01313717 0.009662147 0.010060034 0.008455193
11 500 0.01243118 0.008013833 0.008332143 0.006922989
12 800 0.01294981 0.005382663 0.005581606 0.004541194
13 1000 0.01418090 0.004448188 0.004607343 0.003716602
円環コイルとして計算した値が正解だとすると、
形状比 x がとても大きいところでは
Knよりも むしろ est のほうが正解に近い傾向があります。
誤差は2割位と大きいのですが。
グラフの黒い線がKnです。

【921_nagaoka_est_bigX.png : 8.4KB】
1,348 hits
|
森のカエル - 21/2/4(木) 1:15 - |
散発ですみません。
グラフの傾向がわかりやすいように縦軸を対数にしてみました。
黒 - Kn
赤 - Ko
緑 - Ka
青 - est
です。
表が見にくかったので再掲します。(左に余計な番号が入ってました)
x Kn ko ka est
10 0.20332352 0.151644525 0.167560020 0.199371866
20 0.12361481 0.097885823 0.105843570 0.115543783
50 0.06108325 0.050820905 0.054004004 0.053275065
100 0.03465223 0.029823165 0.031414714 0.029052723
150 0.02470410 0.021602957 0.022663990 0.020289333
200 0.01967690 0.017117938 0.017913713 0.015707634
250 0.01678334 0.014262581 0.014899201 0.012872607
300 0.01499930 0.012272383 0.012802899 0.010937568
350 0.01386311 0.010799572 0.011254300 0.009528808
400 0.01313717 0.009662147 0.010060034 0.008455193
500 0.01243118 0.008013833 0.008332143 0.006922989
800 0.01294981 0.005382663 0.005581606 0.004541194
1000 0.01418090 0.004448188 0.004607343 0.003716602
さらに、x>250のあたりでは、
(2 / (2+x))^0.9 の式を(2 / (2+x))^0.87 とすると
概ね正解(Ko,Ka) に近い値が出ます!!
x=400 - 800 のあたりで 1-2%程度に収まる
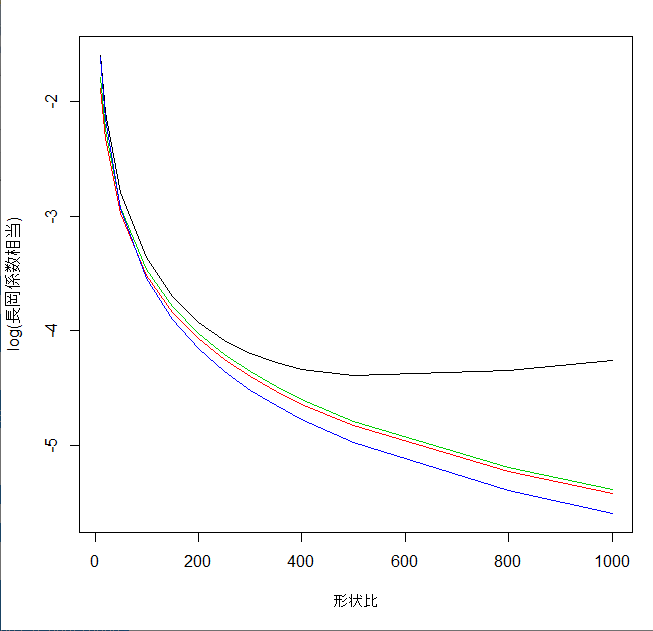
【922_nagaoka_est_bigX_log.png : 9.4KB】
グラフの傾向がわかりやすいように縦軸を対数にしてみました。
黒 - Kn
赤 - Ko
緑 - Ka
青 - est
です。
表が見にくかったので再掲します。(左に余計な番号が入ってました)
x Kn ko ka est
10 0.20332352 0.151644525 0.167560020 0.199371866
20 0.12361481 0.097885823 0.105843570 0.115543783
50 0.06108325 0.050820905 0.054004004 0.053275065
100 0.03465223 0.029823165 0.031414714 0.029052723
150 0.02470410 0.021602957 0.022663990 0.020289333
200 0.01967690 0.017117938 0.017913713 0.015707634
250 0.01678334 0.014262581 0.014899201 0.012872607
300 0.01499930 0.012272383 0.012802899 0.010937568
350 0.01386311 0.010799572 0.011254300 0.009528808
400 0.01313717 0.009662147 0.010060034 0.008455193
500 0.01243118 0.008013833 0.008332143 0.006922989
800 0.01294981 0.005382663 0.005581606 0.004541194
1000 0.01418090 0.004448188 0.004607343 0.003716602
さらに、x>250のあたりでは、
(2 / (2+x))^0.9 の式を(2 / (2+x))^0.87 とすると
概ね正解(Ko,Ka) に近い値が出ます!!
x=400 - 800 のあたりで 1-2%程度に収まる

【922_nagaoka_est_bigX_log.png : 9.4KB】
1,799 hits
|
M2019J1 - 21/8/26(木) 21:25 - |
カエルさん
過日は論点が近似式でないところにズレてしまい失礼しました。
長岡係数によるコイルのインダクタンス計算の補正について、
・近似式を導く考え方
(公知例:テイラー展開、フーリエ級数等)
・実測値と計算値の違い、実測値と計算値の誤差精度
・計算式へのパラメータの適用限界の値域
等がわかるともっと良いかもしれないと思います。
学校では、物理と電磁気学の最初のころにでてくる課題と
記憶していますが、長岡先生の式は、巻数のNが
ちょっと変わった単位で実計算には使いづらいと感じていました。
長岡先生の時代は20世紀はじめあたりで、多分、電卓も電子計算機も無く
実数計算が難しかったと思います。
動画サイトの物理演習問題では長岡係数を無視した近似計算で
学問としては必ずしも実用的または進歩的でないものも
あるので、見直しのチャンスかもですね。
学会誌等へ論文にして発表し、歴史に記憶させるのも良い
ように思いました。
過日は論点が近似式でないところにズレてしまい失礼しました。
長岡係数によるコイルのインダクタンス計算の補正について、
・近似式を導く考え方
(公知例:テイラー展開、フーリエ級数等)
・実測値と計算値の違い、実測値と計算値の誤差精度
・計算式へのパラメータの適用限界の値域
等がわかるともっと良いかもしれないと思います。
学校では、物理と電磁気学の最初のころにでてくる課題と
記憶していますが、長岡先生の式は、巻数のNが
ちょっと変わった単位で実計算には使いづらいと感じていました。
長岡先生の時代は20世紀はじめあたりで、多分、電卓も電子計算機も無く
実数計算が難しかったと思います。
動画サイトの物理演習問題では長岡係数を無視した近似計算で
学問としては必ずしも実用的または進歩的でないものも
あるので、見直しのチャンスかもですね。
学会誌等へ論文にして発表し、歴史に記憶させるのも良い
ように思いました。
1,570 hits
|
森のカエル - 21/8/29(日) 10:01 - |
RFWに載っけていただきました。
近似式で表現すると、形状や半径で微分したりできて、
より直感的に捉えやすいと思います。
ありがとうございました。
▼M2019J1さん:
>
>動画サイトの物理演習問題では長岡係数を無視した近似計算で
>学問としては必ずしも実用的または進歩的でないものも
>あるので、見直しのチャンスかもですね。
>学会誌等へ論文にして発表し、歴史に記憶させるのも良い
>ように思いました。
近似式で表現すると、形状や半径で微分したりできて、
より直感的に捉えやすいと思います。
ありがとうございました。
▼M2019J1さん:
>
>動画サイトの物理演習問題では長岡係数を無視した近似計算で
>学問としては必ずしも実用的または進歩的でないものも
>あるので、見直しのチャンスかもですね。
>学会誌等へ論文にして発表し、歴史に記憶させるのも良い
>ように思いました。
1,627 hits
|
森のカエル - 21/9/28(火) 18:33 - |
落ち穂拾いです。
その後、次の式をみつけました。
Kz = ( 997 + 15 * X)/( 1000 + 471 * X);
kz は インダクタンス計算を意識して、Kz=長岡係数×μ0×π/4 ×10^6 としたものです。
直径をD(m)とすれば、 L = (D*N^2) * X* Kz [uH] となります。
直径28mm, 長さ62mm 20Tならば
x = 28/62
L = x*(997 + 15*x)/(1000 + 471*x) * 0.028 * 20^2
= 4.18662 [uH]
式の中の定数について、
977 と 1000 は μ0×π/4 ×10^6 (=0.9974567..) から来ています。
15 と 471は網羅的に探しました。
この形の式だと Xが大きくなると誤差が拡大してしまうのですが、
X<20の範囲で使えれば、かなり有用と思います。
背景。
知人に、昭和40年代の書籍からインダクタンスの簡易計算式を教えてもらいました。
L = (D*N^2)/(102 / X + 45)
この式は精度も荒く適用範囲も狭いのですが、
これをもとににらめっこして、冒頭の式を得ました。
冒頭のと同じ、または似た式をご存知でしたら教えて下さい。
その後、次の式をみつけました。
Kz = ( 997 + 15 * X)/( 1000 + 471 * X);
kz は インダクタンス計算を意識して、Kz=長岡係数×μ0×π/4 ×10^6 としたものです。
直径をD(m)とすれば、 L = (D*N^2) * X* Kz [uH] となります。
直径28mm, 長さ62mm 20Tならば
x = 28/62
L = x*(997 + 15*x)/(1000 + 471*x) * 0.028 * 20^2
= 4.18662 [uH]
式の中の定数について、
977 と 1000 は μ0×π/4 ×10^6 (=0.9974567..) から来ています。
15 と 471は網羅的に探しました。
この形の式だと Xが大きくなると誤差が拡大してしまうのですが、
X<20の範囲で使えれば、かなり有用と思います。
背景。
知人に、昭和40年代の書籍からインダクタンスの簡易計算式を教えてもらいました。
L = (D*N^2)/(102 / X + 45)
この式は精度も荒く適用範囲も狭いのですが、
これをもとににらめっこして、冒頭の式を得ました。
冒頭のと同じ、または似た式をご存知でしたら教えて下さい。
1,300 hits
60,655